UNO SGUARDO ALLE CONOSCENZE EGIZIE

Di Ivo Prezioso

INTRODUZIONE

A questo punto, è opportuno affrontare il problema sulle reali conoscenze tecniche degli egizi. Sull’argomento si sono versati fiumi di inchiostro e avanzate le teorie più disparate, dalle più plausibili a quelle più astruse e sensazionalistiche. In realtà, la documentazione in merito di cui disponiamo ad oggi è piuttosto limitata, ma le scoperte nella terra dei faraoni sono all’ordine del giorno e, molto probabilmente le ricerche, condotte in modo rigorosamente scientifico, permetteranno di comprendere in maniera sempre più approfondita e precisa le metodologie progettuali e costruttive adottate in un passato così remoto.

Gli scribi egiziani si sono certamente affidati alle loro conoscenze geometriche e matematiche per progettare e sviluppare un’architettura così grandiosa. Estremamente pratici e concreti, non sembra nutrissero una particolare propensione per l’astrazione. Probabilmente, riferendosi a questo popolo di costruttori e agricoltori, inquadrato in un sistema amministrativo rigoroso, è decisamente più appropriato parlare di matematica applicata. La scarsa documentazione giunta sino a noi, cui accennavo in precedenza, è sicuramente da attribuirsi all’estrema fragilità del papiro ed è un caso davvero fortunato che alcune raccolte, come il papiro Rhind (Immagine n. 1) e quello di Mosca (Immagine n. 2), abbiano potuto resistere alle ingiurie del tempo.

Si tratta di due esemplari che datano alla fine del Medio Regno ed entrambi comprendono una serie di esercizi, principalmente di natura contabile e geometrica, che trovavano larga applicazione pratica nella vita quotidiana. Da soli costituiscono la stragrande maggioranza del corpo dei problemi matematici egizi che ci sono noti, dalle origini al Nuovo Regno. Vi sono esposti numerosi enunciati seguiti dalle relative soluzioni e sei di essi sono relativi a problemi legati alle piramidi.

Anche se molto posteriori alla IV dinastia, alcune affermazioni si riferiscono ai calcoli della pendenza delle facce di una piramide (il seqed), le cui caratteristiche sono tipiche di quell’epoca. In particolare, il problema n. 56 del papiro Rhind ha la finalità di determinare il seqed di una piramide di 250 cubiti (131 metri) di altezza e di 360 cubiti (188,64 metri) di lato di base. La soluzione riporta il risultato di 5 palmi e 1/25 (vale a dire, un’inclinazione equivalente a 54°15’). Sono valori che si approssimano in maniera estremamente rimarchevole per dimensioni e proporzioni a quelli della Piramide romboidale di Dashur (IV dinastia) allorché la costruzione era ancora al suo secondo stadio. I dati relativi ai problemi n. 57 e 58, sono invece del tutto identici alle dimensioni della piramide di Userkaf a Saqqara (V dinastia). Questo parallelismo indica, con tutta probabilità, un chiaro legame tra l’architettura dell’ Antico Regno ed i problemi matematici della fine del Medio Regno dal momento che nessun monumento di quest’ ultimo periodo offre un possibile paragone. Tutto ciò lo si può spiegare solo ammettendo una fonte documentaria che si è protratta per diversi secoli, ma della quale purtroppo non rimane nulla.

MISURAZIONI E PENDENZA (SEQED)

L’unità di misura utilizzata dagli antichi egizi per il progetto dei loro edifici era il “cubito reale” e i suoi sottomultipli, il palmo e le dita. Un cubito reale era equivalente a 7 palmi, ovvero 28 dita. Non utilizzavano gli angoli, così come li conosciamo, per esprimere un’inclinazione. Si avvalevano di un rapporto di pendenza in cui la differenza di livello era sempre fissata a un cubito (ossia 7 palmi). Il seqed era il denominatore di questo rapporto che si esprimeva attraverso una misura di lunghezza. Ad esempio, il seqed di un angolo di 54°27’ corrispondeva a 5 palmi; Il seqed di 42°5’ a 1 cubito e 3 dita (ovvero 7 palmi e 3 dita) ecc. (Immagine n. 3).

A causa della mancanza di documentazione coeva, è fiorita tutta una letteratura sulle presunte proprietà matematiche delle piramidi e l’immaginazione, più che la ragione, ha dato la stura ad ogni sorta di divagazione. Così, saltano fuori presunte relazioni geometriche celate nell’architettura della Grande Piramide di Cheope (chissà perché sempre e solo in quella, come se fosse l’unica esistente in Egitto!) in cui il numero aureo ϕ, oppure π occupano un ruolo preponderante.

I documenti di cui siamo in possesso non fanno alcun accenno, sia pure vago, a π: certamente non era noto, né impiegato dagli egizi almeno fino alla fine del Medio Regno. Ciò, d’altra parte, non deve essere interpretato come la prova di una scienza rozza e primitiva. Gli scribi avevano semplicemente trovato un diverso, semplice modo per calcolare l’area di un cerchio, avendo notato che essa corrispondeva (all’incirca) a quella di un quadrato avente i lati più corti di un nono rispetto al diametro. E’ un procedimento del tutto differente, ma altrettanto efficace per le loro esigenze. Il risultato era un poco diverso in quanto equivalente a quello ottenuto applicando un valore di π pari a circa 3,16. (Immagini n. 4-5)

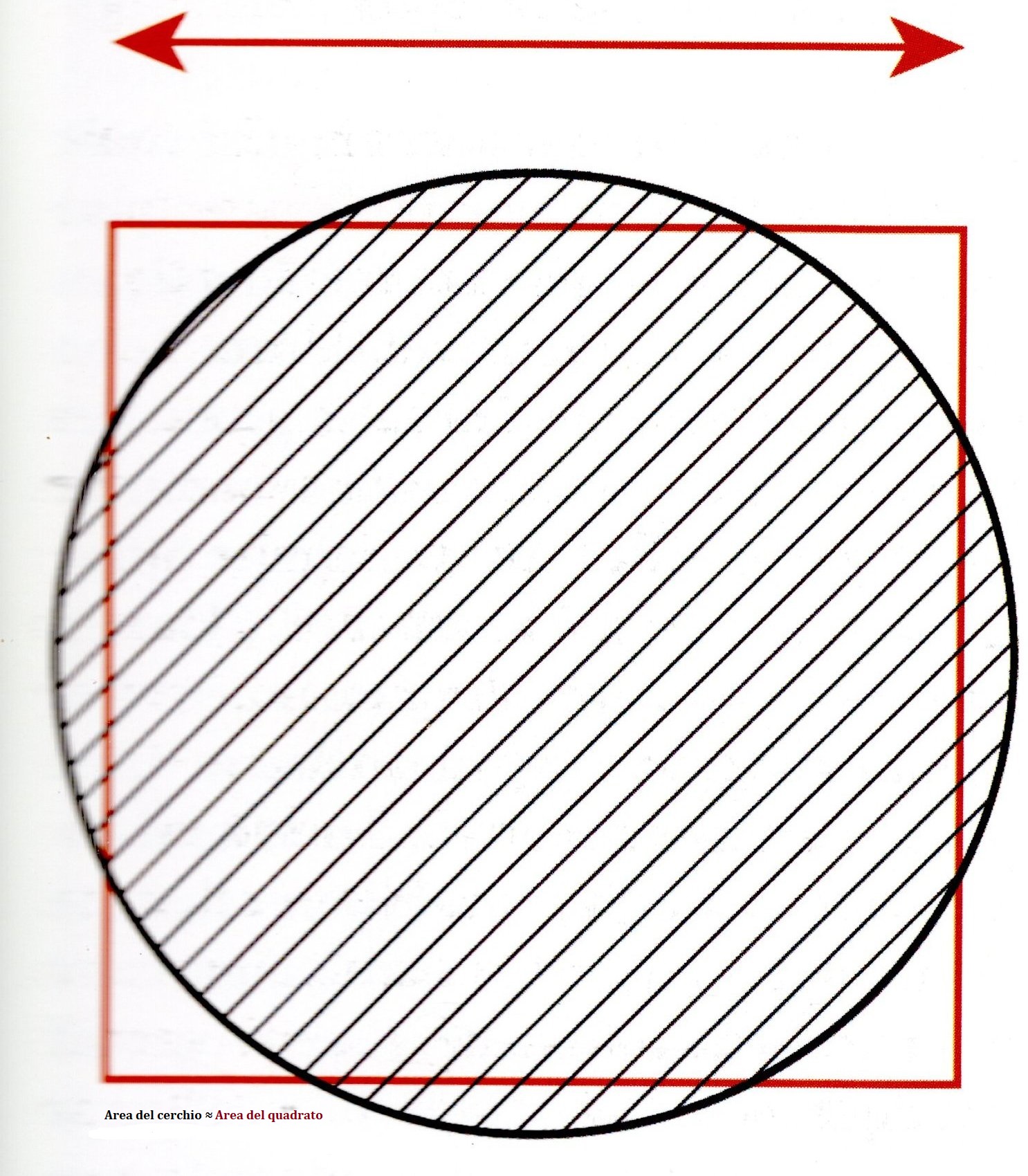
Calcoliamo, ad esempio, l’area di un cerchio avente diametro 10 cm. (ossia una raggio pari a 5 cm.)

Applicando la formula che ci è nota fina dalle scuole elementari abbiamo:
πrr= 3,14×25= 78,50 cmq

Utilizzando il metodo degli antichi egizi abbiamo:
(10-10/9)x(10-10/9)= (10-1,11)x(10-1,11)= 8,89×8,89= 79,03 cmq.

L’irrazionalità del valore di π è stata stabilita solo in epoca moderna, pertanto l’importanza quasi metafisica che oggigiorno gli viene attribuita da taluni non aveva alcuna ragione di esistere nelle scuole greche, né tantomeno, e a maggior ragione, in quelle degli egizi dell’ Antico Regno, che addirittura ne ignoravano l’esistenza.

Quanto al numero o sezione aurea ϕ, nessun documento ci autorizza a pensare che, all’epoca, se ne avesse una sia pur vaga nozione. Come per π, si tratta di una coincidenza fortuita scaturita dalla scelta di un semplice rapporto di pendenza per controllare l’inclinazione delle facce. Appare ovvio che i “mistici” che vedono la piramide di Khufu come un monumento unico che concentra gli elementi di una conoscenza superiore e nascosta si sbagliano nel considerarla sotto questa luce. La sua pendenza trae origine dalla piramide, eretta a Meidum, dal padre Snefru, edificio che è il risultato di due modifiche successive rispetto al progetto iniziale.

E che dire delle svariate figure geometriche che secondo alcuni sono alla base della planimetria interna degli edifici e la cui complessità “alchemica”, indizio lampante di schemi “rivelati”, ha un senso unicamente per quegli autori ostinatamente convinti di averne ricavato la prova di un sapere dimenticato o di un messaggio nascosto? In realtà, le piramidi si avvalevano di pendenze semplici e variabili e le correlazioni tra figure geometriche e schemi architettonici sono di scarsa utilità dal momento che non è possibile farsene un’idea senza il ricorso ad un massiccio impiego di ipotesi.

ORIENTAMENTO E CONOSCENZE ASTRONOMICHE

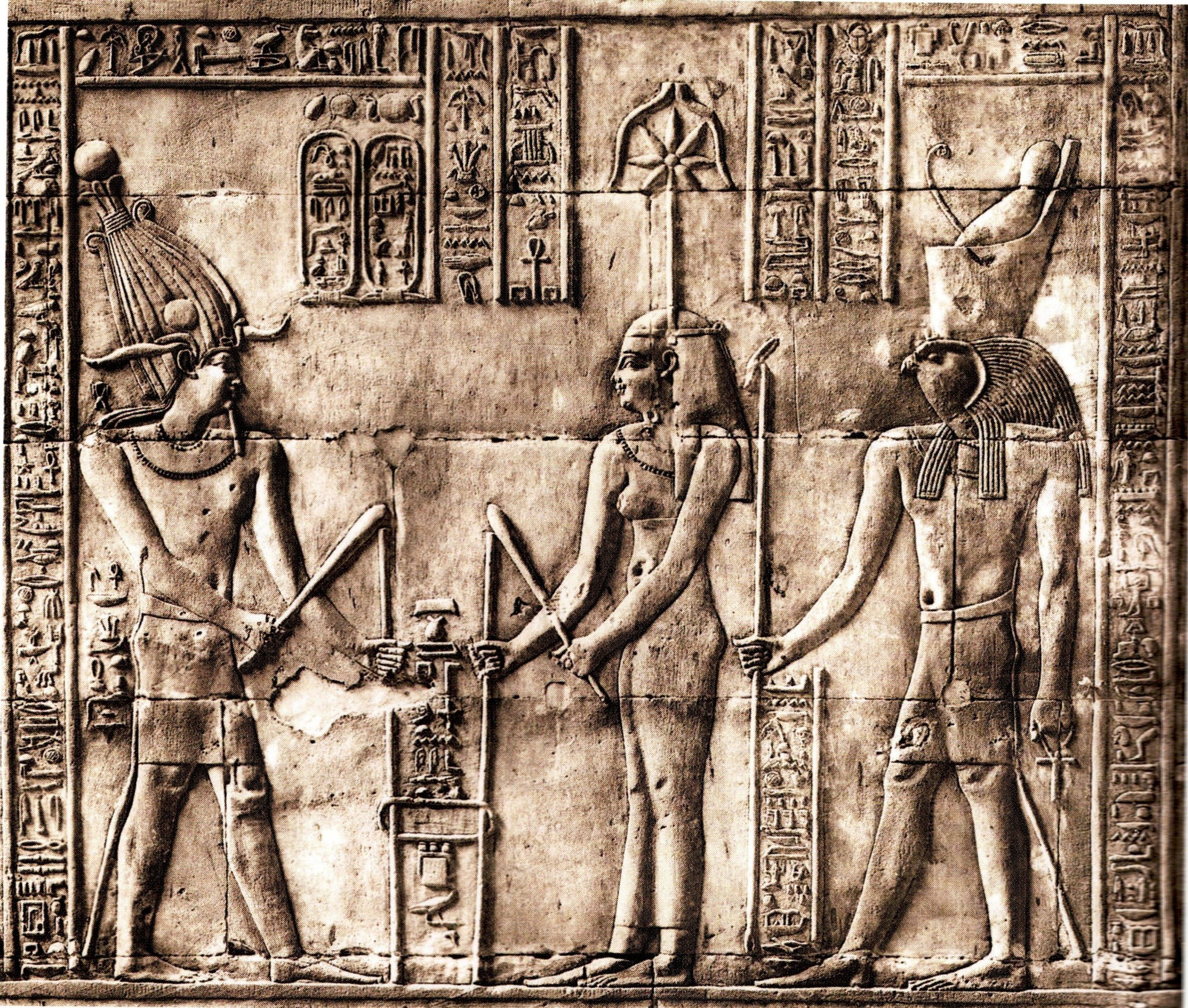
Come per la matematica, ciò che sappiamo in merito alle conoscenze astronomiche lo si apprende da fonti più tarde (posteriori al Secondo Periodo Intermedio). Tuttavia, i collegamenti tra le piramidi e le osservazioni della volta celeste non sono, per questo, da scartare. Si sa che, durante l’Antico Regno, l’orientamento degli edifici ha costantemente come riferimento il nord e punta verso la regione circumpolare dell’emisfero boreale. Gli studiosi concordano pressoché unanimemente sul significato religioso di questa disposizione che avrebbe permesso all’anima del sovrano di ricongiungersi con le stelle che “non tramontano mai”. Inoltre, testi di epoca tarda descrivono tradizionali cerimonie di fondazione durante le quali il posizionamento di un monumento, in base alla posizione degli astri, giocava un ruolo di grande importanza (Immagine n. 6). È senza dubbio durante il rituale della “tensione della corda” che venivano gettate le fondamenta di una piramide, prestando particolare attenzione a orientarla secondo i quattro punti cardinali.

Nessun documento ci è pervenuto, al momento, che possa fornirci chiarimenti sui metodi impiegati. A causa della precessione degli equinozi, la Stella Polare, agli inizi dell’ Antico Regno, non era quella a cui ci riferiamo oggi (Alpha dell’ Orsa Minore), ma un punto del cielo situato a meno di 2° da Thuban (la stella Alpha della costellazione del Dragone). Questa stella era quindi troppo lontana per fornire un risultato soddisfacente in relazione alla precisione osservata (Immagine n. 7).

I ricercatori, che si sono interessati al problema dell’orientamento, hanno proposto svariate tecniche verosimili che avrebbero permesso di determinare con precisione la direzione del nord utilizzando i mezzi dell’epoca. Una di queste suggerisce una meticolosa osservazione notturna della posizione degli astri. Determinando la levata ed il tramonto di una stella, gli egizi avrebbero potuto ottenere l’esatta direzione del nord. Era però necessario ricreare una linea dell’orizzonte perfettamente orizzontale per godere di condizioni di osservazione ottimali.

In tempi più recenti, Kate Spence ha evidenziato un’evoluzione lineare delle differenze di orientamento nelle piramidi erette tra la IV e l’inizio della V dinastia che l’ha portata a concludere che gli architetti avevano utilizzato la volta stellata come punto di riferimento. Un indicatore che, con il passare dei decenni, si è prima avvicinato al polo e poi, in modo sempre più consistente, vi si è rapidamente allontanato a causa della precessione degli equinozi. Secondo l’egittologa britannica, i geometri, muniti di filo a piombo, avrebbero scelto di prendere come punto di riferimento le stelle Mizar (Orsa maggiore) e Kochab (Orsa Minore), aspettando che si allineassero verticalmente (Immagine n. 8).

All’epoca il polo celeste corrispondeva all’allineamento dei queste due stelle e, pertanto, è probabile che gli egizi lo individuassero in questo modo. Con il progressivo spostamento dell’asse di rotazione terrestre e l’allontanamento di questi due astri dal polo, il margine di errore sarebbe divenuto sempre più ampio e reso i riferimenti inadeguati.

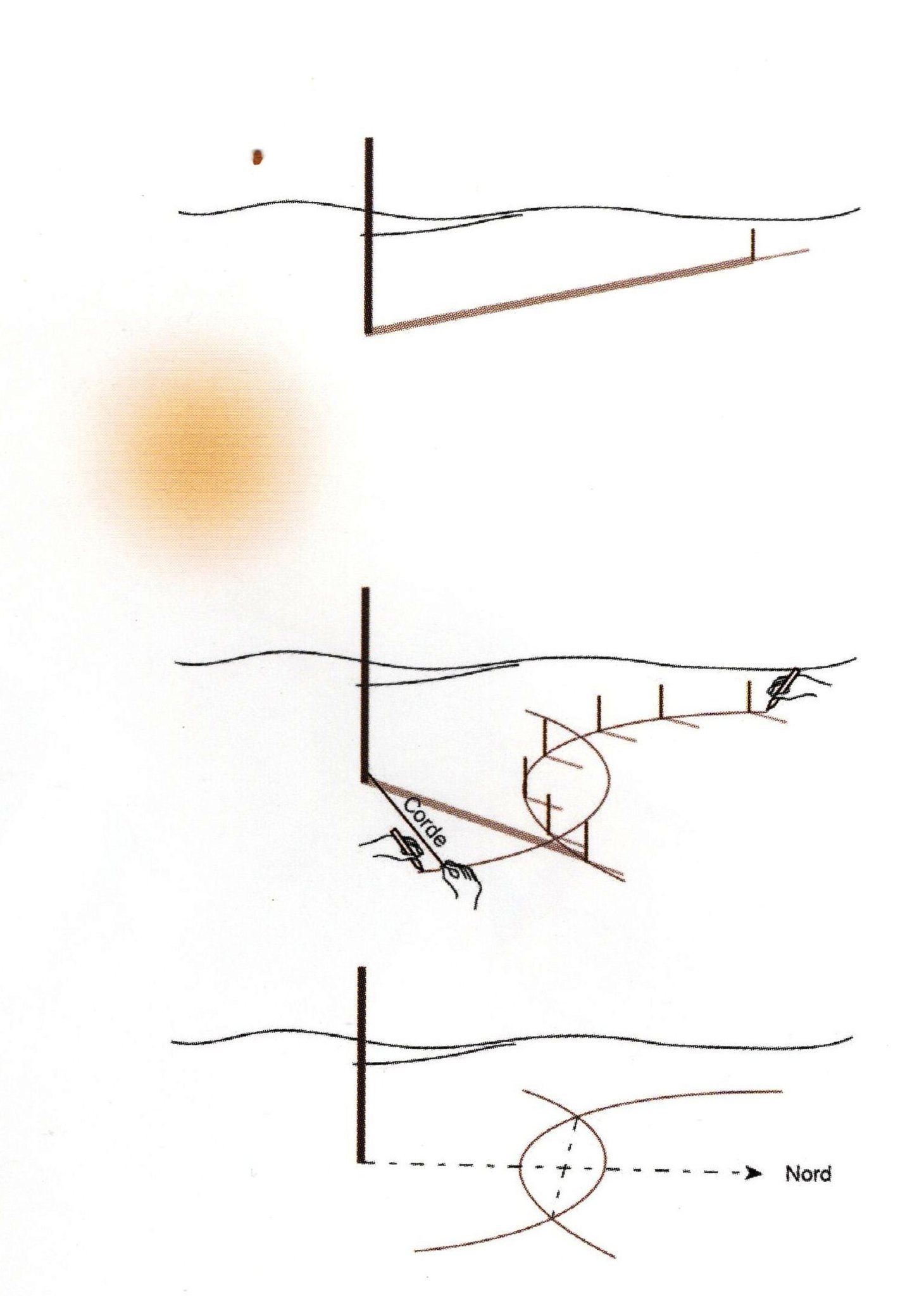
Il nord avrebbe anche potuto essere determinato attraverso osservazioni diurne, contrassegnando, su un suolo perfettamente livellato, le ombre proiettate da una pertica in momenti opposti della giornata (levata e tramonto del sole). La bisettrice dell’angolo che veniva a formarsi avrebbe indicato la direzione (Immagine n. 9).

Oltre a orientare la piramide, la fase preparatoria consisteva nel tracciarne i confini, stabilirne gli angoli e livellare la piattaforma su cui doveva essere eretta. I geometri e gli agrimensori egizi hanno dimostrato anche in questo caso tutta la loro abilità, poiché gli angoli retti della Grande Piramide sono pressoché perfetti, con uno scarto medio di 3’38″ e il dislivello della base fa segnare uno stupefacente valore di soli 2,10 centimetri!

La perfetta orizzontalità dei lati, con molta probabilità, fu ottenuta mediante un piano di riferimento rigorosamente livellato e punti di riscontro situati ai quattro angoli della struttura. Confrontandoli l’uno rispetto agli altri, permise di allinearli, asportando gradualmente il suolo roccioso fino ad ottenere una superficie del tutto piana. La geometria dell’epoca permetteva sicuramente di risolvere il problema della perpendicolarità degli angoli, anche se la presenza dell’enorme massa rocciosa impediva, ovviamente, di avvalersi del tracciamento delle diagonali. Ci si poteva,pertanto, basare unicamente su misure prese lungo il perimetro esterno. Intorno alle piramidi di Khufu e Khaefra furono scavate buche circolari o quadrate per ospitare dei marcatori distanziati di 3-5 metri. Questi fornivano un grosso riferimento nel mantenere la linearità dei lati, ma è probabile che giocassero un ruolo altrettanto importante nel tracciamento di angoli perfettamente ortogonali (Immagine n. 10).

Gli egizi dimostrano di avere avuto una buona conoscenza del comportamento delle strutture, sia in termini di resistenza dei materiali sia nello studio della loro stabilità. Questo è senz’altro uno degli aspetti più rivoluzionari e sorprendenti che si riscontrano nella loro architettura. Le tecnologie che misero a punto suscitano enorme ammirazione soprattutto in considerazione dei rudimentali mezzi di cui disponevano e della limitatezza delle loro conoscenze teoriche. Queste conquiste furono il risultato di un percorso empirico e pragmatico intrapreso da tecnici tenaci e desiderosi di vincere la sfida posta dal sovrano e dai suoi architetti, mentre la mancanza di basi scientifiche fu compensata dalle ampie risorse messe a loro disposizione.

Alcuni componenti dell’edificio furono progettati e realizzati prima di essere trasferiti in cantiere: è il caso, ad esempio, delle volte e delle coperture su cui si sarebbe retto l’equilibrio della distribuzione interna (Immagine n. 11).

Altrettanto si può dire dei sistemi di bloccaggio e sigillatura delle tombe che, senza alcun dubbio, venivano sperimentati in precedenza, così come sembrerebbe dimostrare il sistema di passaggi in miniatura (la cosiddetta “maquette”) scoperto nei pressi della Grande Piramide* (Immagini n. 12-13).

Quando gli egizi decisero di innalzare questi edifici, dovettero, al contempo, elaborare un’architettura in grado di sfidare il tempo. I primi stadi della piramide di Djoser a Saqqara, rivelano che fu durante la sua costruzione che fu inventata la struttura a “piani rovesciati”. I muri con fianchi inclinati esistevano già da lungo tempo, ma, evidentemente, furono ritenuti insufficientemente stabili per utilizzarli in questo tipo di monumento. La piramide a gradoni è costituita da un tronco centrale il cui profilo è simile alla muratura con pareti inclinate, ma con le basi inclinate verso il centro invece che essere orizzontali. A questo tronco sono addossati contrafforti avvolgenti montati allo stesso modo. Gli sforzi si trasmettevano così verso l’interno dell’edificio e comprimevano gli elementi della costruzione impedendo che potessero scivolare verso l’esterno. I blocchi che compongono l’edificio sono squadrati, ma le facce sono solo approssimativamente verticali.

In seguito, quando si decise di posare le pietre in corsi orizzontali, si capì chiaramente che i basamenti dovevano essere perfettamente piani per non comprometterne la stabilità. Fu necessario neutralizzare il rischio di assestamenti localizzati e di scivolamento laterale della muratura (Immagine n. 14).

La piramide di Meidum evidenzia molto bene la differenza qualitativa della muratura tra le sezioni interne, dove si riscontrano notevoli differenze di livello, e quelle dell’involucro esterno, dove le fondazioni sono livellate con un errore di soli 8,30 centimetri. Le ragioni del passaggio da una piramide a gradoni con corsi rovesciati ad una a facce lisce con corsi orizzontali sono, probabilmente, sia di natura tecnica, sia religiosa; ancora però non è chiaro in quale misura l’una sia in relazione o prevalga sull’altra. E’ però ipotizzabile che l’impiego di blocchi sempre più voluminosi abbia costretto i direttori dei lavori a rinunciare all’inclinazione verso l’interno dei piani di posa.

Lo studio dei comportamenti di un edificio ci ha permesso di comprendere che i costruttori impararono presto a non preoccuparsi troppo delle crepe che comparivano durante l’ edificazione. I massicci architravi che coprono i corridoi sono molto spesso fratturati, ma questo non impedì agli egizi di metterli ugualmente in opera. Del resto, portarono a compimento l’erezione della piramide romboidale di Dashur-Sud, nonostante i grandi cambiamenti strutturali che intervennero ben prima della fine del progetto. Questo dimostra che avevano la capacità di valutare l’incidenza dei danni e dei sommovimenti della struttura e di decidere di conseguenza sulle azioni da intraprendere.

*I corridoi del cosiddetto “Passaggio di prova” sono quasi identici, per sezione e orientamento, ai corridoi della Piramide di Khufu, solo in scala ridotta di circa 1:5. Inoltre, sono stati realizzati gli incavi per la copertura delle tavole, il che fa supporre che la funzionalità dei blocchi di chiusura sia stata testata sul modello. All’estremità inferiore del passaggio sud è stata lasciata una piccola sporgenza di roccia, che doveva impedire ai blocchi di chiusura di scivolare nel passaggio in uscita, in modo che rimanesse possibile per i sacerdoti lasciare la piramide dopo la sepoltura e la chiusura. Questo elemento di chiusura non è stato adottato nella struttura originale. Al contrario, la navata fu resa più stretta di 2 cm, in modo che i blocchi di chiusura si bloccassero in questo punto. Questo è visibile ancora oggi su due blocchi originali.

Gli architetti di questa struttura hanno imitato il corridoio discendente, il corridoio ascendente, la parte inferiore della Grande Galleria e anche il corridoio orizzontale che conduce alla Camera della Regina. Questo sistema fu scoperto da Vyse e Perring e da questi esaminato e rilevato. Quando, nel 1990, l’altopiano orientale della Piramide di Khufu è stato ripulito dalle macerie e dalla sabbia, anche il modello di “passaggio di prova” è stato riportato alla luce. (Fonte: https://nefershapiland.de/Cheops-Pyramide.htm)

Fonte: Franck Monnier “L’Univers Fascinant des Piramides d’Égypte”, pag.209